ত্রিভুজ

ত্রিভুজ হল সমতলের উপর অঙ্কিত একটি চিত্র যা তিনটী সরলরেখা দ্বারা সীমাবদ্ধ। যদি ত্রিভুজের তিনটি বাহুই অসম হয়, তবে একে বিষমবাহু ত্রিভুজ বলে। আর কেবল দুই বাহু সমান হলে তাকে সমদ্বিবাহু ত্রিভুজ এবং তিনটি বাহুই সমান হলে তাকে সমবাহু ত্রিভুজ বলা হয়। সমদ্বিবাহু ত্রিভুজে সমান বাহুদ্বয়ের বিপরীত কোণগুলি সমান। আর সমবাহু ত্রিভুজের সবগুলি কোণ সমান।

যে ত্রিভুজের একটি কোন সমকোণ তাকে সমকোণী ত্রিভুজ বলে। সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুর নাম অতিভুজ। পিথাগোরাসের বিখ্যাত উপপাদ্য অনুযায়ী সমকোণী ত্রিভুজের অতিভুজের বর্গ এর সমকোণ-সংলগ্ন দুই বাহুর বর্গের যোগফলের সমান। অর্থাৎ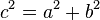 

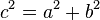
ত্রিভুজের ভিতরের কোনগুলিকে অন্তঃস্থ কোণ বলে, আর ত্রিভুজের বাহুগুলিকে বাড়িয়ে দিয়ে যে কোণগুলি পাওয়া যায়, তাদেরকে হলে বহিঃস্থ কোণ। ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি ১৮০°। এছাড়াও, যেকোন বহিঃস্থ এর অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান।

ত্রিভুজের কোন শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত আঁকা রেখাকে বলা হয় ত্রিভুজটির একটি মধ্যমা। ত্রিভুজের তিনটি মধ্যমা একই বিন্দুতে ছেদ করে এবং এটি প্রতিটি মধ্যমার শীর্ষবিন্দু থেকে দুই-তৃতীয়াংশ দূরত্বে অবস্থিত। ত্রিভুজের কোন শীর্ষবিন্দু থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বকে ঐ ত্রিভুজের উচ্চতা বলে।

দুইটি ত্রিভুজকে সর্বসম বলা হয় যদি এগুলি নিচের তিনটি শর্তের সেটের যেকোনটি পূরণ করে: (১) একটি ত্রিভুজের এক বাহু ও দুইটি কোণ অন্যটির অনুরূপ বাহু ও দুইটি কোনণর সমান; (২) কোন একটি ত্রিভুজের দুই বাহু এবং এদের অন্তর্ভুক্ত কোণ অন্য ত্রিভুজটির দুই বাহু ও অন্তর্ভুক্ত কোণের সমান; অথবা (৩) একটি ত্রিভুজের তিনটি বাহু অপর ত্রিভুজের তিন বাহুর সমান। যদি একই সমতলে অবস্থিত দুইটি ত্রিভুজকে নিখুঁতভাবে একটির উপর আরেকটিকে বসিয়ে দেয়া যায়, তবে তারা সরাসরি সর্বসম। আর যদি বসানোর আগে একটিকে উল্টে নিতে হয়, তবে ত্রিভুজ দুটি বিপরীতভাবে সর্বসম।

যদি দুইটি ত্রিভুজের একটির সবগুলি কোণ অন্যটির সবগুলি কোণের সমান হয়, তবে তাদেরকে সদৃশ ত্রিভুজ বলা হয় এবং এদের অনুরূপ বাহুগুলি সমানুপাতিক হয়।

ত্রিভুজের ক্ষেত্রফল এর ভূমি (b) ও এই ভূমির উপর অঙ্কিত উচ্চতার (h) গুণফলের অর্ধেক ()। যেকোন বাহুকেই ভূমি ধরা যায়। যদি ত্রিভুজটি সমবাহু হয়, তবে এর ক্ষেত্রফল , যেখানে a যেকোন বাহুর দৈর্ঘ্য। যদি কোন ত্রিভুজের তিনটি বাহু a, b এবং c হয়, তবে গ্রিক গণিতবিদ আর্কিমিডিসের দেয়া সূত্র অনুযায়ী এর ক্ষেত্রফল , যেখানে s ত্রিভুজের পরিসীমার অর্ধেক (s = ½ (a + b + c)।

চতুর্ভুজ

চতুর্ভুজ হল চারটি সরলরেখা দ্বারা আবদ্ধ সমতল ক্ষেত্র। যেসব বিভিন্ন চতুর্ভুজের সাথে আমরা অতিপরিচিত তাদের মধ্যে আছে ট্রাপিজিয়াম, যার দুইটি সমান্তরাল কিন্তু অসমান। সামান্তরিকের বিপরীত বাহুগুলি সমান ও সমান্তরাল। রম্বস এক ধরনের সামান্তরিক যার সবগুলি বাহু সমান। আয়তক্ষেত্র এক ধরনের সামান্তরিক যার কোণগুলি সমকোণ। বর্গক্ষেত্র হল সমান বাহুবিশিষ্ট আয়তক্ষেত্র। সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে। আয়োতক্ষেত্রের কর্ণদ্বয় সমান। যেসব চতুর্ভুজের বাহুগুলি অসমান ও অসমান্তরাল, তাদেরকে বিষম চতুর্ভুজ বলে।

ট্রাপিজিয়ামের ক্ষেত্রফল এর সমান্তরাল বাহুদ্বয়ের সমষ্টি ও উচ্চতার গুণফলের অর্ধেক: A = [(b1 + b2)/2]h। সামান্তরিকের ক্ষেত্রফল এর ভূমি ও উচ্চতার গুণফলের সমান: A = bh।

বিষম চতুর্ভুজের ক্ষেত্রফল গণনার জন্য চতুর্ভুজটিকে সাধারণত কর্ণের সাহায্যে দুইটি ত্রিভুজে ভাগ করে নেয়া হয় এবং তারপর ত্রিভুজ দুইটির ক্ষেত্রফল আলাদা করে বের করে যোগ করে সম্পূর্ণ চতুর্ভুজের ক্ষেত্রফল বের করা হয়।

ত্রিমাত্রিক ইউক্লিডীয় আকৃতিসমূহ

ত্রিমাত্রিক জ্যামিতিতে যে বস্তুগুলি প্রায়োই আলোচিত হয় তাদের মধ্যে আছে গোলক, বহুতলক, ত্রিশিরা বা প্রিজম, বেলন বা সিলিন্ডার, ও কোণক। বেলন আসলে প্রিজমেরই একটি বিশেষ রূপ; আর কোণক পিরামিডের বিশেষ রূপ।

গোলক

গোলক একটি তল যার সমস্ত বিন্দু কেন্দ্র নামের একটি বিন্দু থেকে সমদূরত্বে অবস্থিত। গোলককে একটি সমতল দিয়ে ছেদ করলে ছেদবিন্দুগুলি একটি বৃত্ত গঠন করে। তলটি গোলকের কেন্দ্র দিয়ে গেলে এরূপ বৃহত্তম বৃত্তটি পাওয়া যায়। পৃথিবীর বিষুবরেখা এরকম একটি বৃহত্তম বৃত্ত (যদি পৃথিবীকে একটি গোলক কল্পনা করি)। গোলকের পৃষ্ঠতলের ক্ষেত্রফল A = 4pr2, এবং আয়তন V = 4/3pr3 সমীকরণ দিয়ে পাওয়া যায়।

বহুতলক

সমতল পৃষ্ঠ দ্বারা আবদ্ধ যেকোন ঘনবস্তুকে বহুতলক বলে। যদি কোন বহুতলকের পৃষ্ঠগুলির প্রতিটি সর্বসম সুষম বহুভুজ হয়, তবে এটিকে সুষম বহুতলক বলা হয়। প্রমাণ করা হয়েছে যে কেবল পাঁচ রকমের বহুতলকের জন্য সুষম বহুতলক সম্ভব। এগুলি হল চতুস্তলক (চারটি তল), ঘনক (ছয়টি তল), অষ্টতলক (আটটি তল), দ্বাদশতলক (১২টি তল), এবং বিশতলক (২০টি তল)। প্রাচীন গ্রিক জ্যামিতিবিদেরা এই পাঁচটি বহুতলক সম্পর্কে জানতেন। সুষম কিংবা অসম, যেকোন বহুতলকের একটি বিশেষ ধর্ম হচ্ছে এর তলের সংখ্যা ও শীর্ষবিন্দুর সংখ্যা যোগ করে ২ বিয়োগ করলে এর ধারের সংখ্যা পাওয়া যায়। সাম্প্রতিককাল পর্যন্তও বহুতলকগুলির সাথে প্রকৃতির রহস্যময়তার সম্পর্ক আছে বলে ধারণা করা হত।

ত্রিশিরা বা প্রিজম

প্রিজম হচ্ছে এমন এক ধরনের বহুতলক যার দুইটি পৃষ্ঠ পরস্পর সমান্তরাল ও সর্বসম (এদেরকে ভূমি বলে) এবং যার অন্য সব পৃষ্ঠ সামান্তরিক। parallelepiped এক ধরনের প্রিজম যার ভূমিদ্বয় সামান্তরিক। একটি সমকোণী প্রিজমের তলগুলি আয়তাকার(ভূমিগুলি আয়তাকার হতেও পারে নাও হতে পারে)। প্রিজমের আয়তন এর যেকোন ভূমির ক্ষেত্রফল ও উচ্চতার গুণফল: V = bh.

পিরামিড

পিরামিড একটি বহুতলক যার ভূমি একটি বহুভুজ এবং পার্শ্বগুলি একই শীর্ষবিন্দুবিশিষ্ট ত্রিভুজ। যদি কোন পিরামিডের ভূমি সুষম বহুভুজ হয় এবং এর শীর্ষ ও ভূমির কেন্দ্রবিন্দুকে সংযোগকারী রেখা ভূমির উপর লম্ব হয়, তবে এটিকে সুষম সমকোণী পিরামিড বলে। পিরামিডের ক্ষেত্রফল এর ভূমির ক্ষেত্রফলের এক-তৃতীয়াংশ ও এর উচ্চতার গুণফলের সমান।

বেলন বা সিলিন্ডার ও কোণক

বেলন বা সিলিন্ডার হল বৃত্তাকার ভূমিবিশিষ্ট প্রিজম। এর আয়তনের সূত্রও তাই প্রিজমের মত ভূমির ক্ষেত্রফল ও উচ্চতার গুণফল দিয়ে বের করা হয়। যদি দুইটি ভূমির কেন্দ্রকে সংযোগকারী রেখা ভূমিদ্বয়ের উপর লম্ব হয়, তবে সেই সিলিন্ডারকে সমকোণী সিলিন্ডার বলা হয়। নতুবা একে তির্যক সিলিন্ডার বলে।

কোণক (cone) হল বৃত্তাকার ভূমিবিশিষ্ট পিরামিড। পিরামিডের শীর্ষ ও ভূমির কেন্দ্রকে সংযোগকারী রেখা ভূমির উপর লম্ব হলে তাকে সমকোণী কোণক বলে। b ক্ষেত্রফলের ভূমি ও h উচ্চতার কোণকের আয়তনের সূত্র পিরামিডের অনুরূপ: V = €bh